卡諾圖是邏輯函數(shù)的一種圖形表示。一個邏輯函數(shù)的卡諾圖就是將此函數(shù)的最小項表達(dá)式中的各最小項相應(yīng)地填入一個方格圖內(nèi)，此方格圖稱為卡諾圖。 卡諾圖的構(gòu)造特點使卡諾圖具有一個重要性質(zhì)：可以從圖形上直觀地找出相鄰最小項。兩個相鄰最小項可以合并為一個與項并消去一個變量。

卡諾圖 （Karnaugh map）

　　卡諾圖是邏輯函數(shù)的一種圖形表示。一個邏輯函數(shù)的卡諾圖就是將此函數(shù)的最小項表達(dá)式中的各最小項相應(yīng)地填入一個方格圖內(nèi)，此方格圖稱為卡諾圖。

　　卡諾圖的構(gòu)造特點使卡諾圖具有一個重要性質(zhì)：可以從圖形上直觀地找出相鄰最小項。兩個相鄰最小項可以合并為一個與項并消去一個變量。

　　用卡諾圖化簡邏輯函數(shù)的基本原理就是把上述邏輯依據(jù)和圖形特征結(jié)合起來，通過把卡諾圖上表征相鄰最小項的相鄰小方格“圈”在一起進(jìn)行合并，達(dá)到用一個簡單“與”項代替若干最小項的目的。

　　在數(shù)字電路中經(jīng)常使用。

　　缺點:當(dāng)變量的數(shù)目超過6時.畫圖就變得復(fù)雜了,也不容易計算.........

用卡諾圖簡化邏輯函數(shù)

　　邏輯函數(shù)未用最小項表示照樣可以化簡。如果F采用與—或表達(dá)式，在填入卡諾圖過程中就能把函數(shù)展開成最小項。

　　具有無關(guān)項的化簡

　　無關(guān)項又叫任意項，是一種最小項，其值可以取0或1。利用無關(guān)項這一特點，可以使函數(shù)簡化。

　　用卡諾圖化簡邏輯函數(shù)的步驟

　　如果表達(dá)式為最小項表達(dá)式，則可直接填入卡諾圖

　　如表達(dá)式不是最小項表達(dá)式，但是“與—或表達(dá)式”，可將其先化成最小項表達(dá)式，再填入卡諾圖。也可直接填入。

　　合并相鄰的最小項，即根據(jù)下述原則畫圈

　　盡量畫大圈，但每個圈內(nèi)只能含有2n（n=0,1,2,3……）個相鄰項。要特別注意對邊相鄰性和四角相鄰性。

　　圈的個數(shù)盡量少。

　　卡諾圖中所有取值為1的方格均要被圈過，即不能漏下取值為1的最小項。

　　在新畫的包圍圈中至少要含有1個末被圈過的1方格，否則該包圍圈是多余的。

　　寫出化簡后的表達(dá)式。每一個圈寫一個最簡與項，規(guī)則是，取值為1的變量用原變量表示，取值為0的變量用反變量表示，將這些變量相與。然后將所有與項進(jìn)行邏輯加，即得最簡與—或表達(dá)式。

　　在進(jìn)行化簡時，如果用圖中真值為0的項更方便，可以用他們來處理，方法和真值取1時一樣，只是結(jié)果要再做一次求反。

變量卡諾圖

　表示各最小項的2^n（n-變量數(shù)）個小格，排列呈矩形。

小格按“循環(huán)碼” 排列，保證最小項間“幾何相鄰”與“邏輯相鄰性”的統(tǒng)一。（幾何相鄰有“內(nèi)相鄰” “外相鄰”和“中心對稱”）

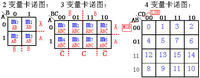
變量卡諾圖