什么是戴維南定理

　　戴維南定理（又譯為戴維寧定理）又稱等效電壓源定律，是由法國科學(xué)家L·C·戴維南于1883年提出的一個(gè)電學(xué)定理。由于早在1853年，亥姆霍茲也提出過本定理，所以又稱亥姆霍茲-戴維南定理。其內(nèi)容是：一個(gè)含有獨(dú)立電壓源、獨(dú)立電流源及電阻的線性網(wǎng)絡(luò)的兩端，就其外部型態(tài)而言，在電性上可以用一個(gè)獨(dú)立電壓源V和一個(gè)松弛二端網(wǎng)絡(luò)的串聯(lián)電阻組合來等效。在單頻交流系統(tǒng)中，此定理不僅只適用于電阻，也適用于廣義的阻抗。戴維南定理在多電源多回路的復(fù)雜直流電路分析中有重要應(yīng)用。

　　戴維南定理（Thevenin‘stheorem）：含獨(dú)立電源的線性電阻單口網(wǎng)絡(luò)N，就端口特性而言，可以等效為一個(gè)電壓源和電阻串聯(lián)的單口網(wǎng)絡(luò)。電壓源的電壓等于單口網(wǎng)絡(luò)在負(fù)載開路時(shí)的電壓uoc；電阻R0是單口網(wǎng)絡(luò)內(nèi)全部獨(dú)立電源為零值時(shí)所得單口網(wǎng)絡(luò)N0的等效電阻。

　　戴維南定理典型例子

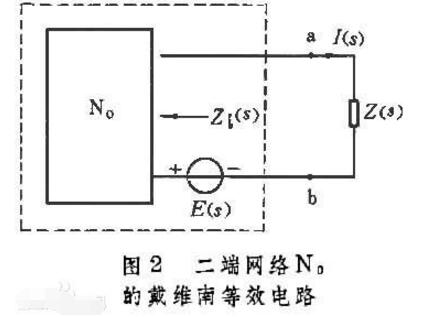
　　戴維南定理指出，等效二端網(wǎng)絡(luò)的電動(dòng)勢(shì)E等于二端網(wǎng)絡(luò)開路時(shí)的電壓，它的串聯(lián)內(nèi)阻抗等于網(wǎng)絡(luò)內(nèi)部各獨(dú)立源和電容電壓、電感電流都為零時(shí)，從這二端看向網(wǎng)絡(luò)的阻抗Zi。設(shè)二端網(wǎng)絡(luò)N中含有獨(dú)立電源和線性時(shí)不變二端元件（電阻器、電感器、電容器），這些元件之間可以有耦合，即可以有受控源及互感耦合；網(wǎng)絡(luò)N的兩端ɑ、b接有負(fù)載阻抗Z（s），但負(fù)載與網(wǎng)絡(luò)N內(nèi)部諸元件之間沒有耦合，U（s）=I（s）/Z（s）。當(dāng)網(wǎng)絡(luò)N中所有獨(dú)立電源都不工作（例如將獨(dú)立電壓源用短路代替，獨(dú)立電流源用開路代替），所有電容電壓和電感電流的初始值都為零的時(shí)候，可把這二端網(wǎng)絡(luò)記作N0。這樣，負(fù)載阻抗Z（s）中的電流I（s）一般就可以按下式1計(jì)算（圖2）式中E（s）是圖1二端網(wǎng)絡(luò)N的開路電壓，亦即Z（s）是無窮大時(shí)的電壓U（s）；Zi（s）是二端網(wǎng)絡(luò)N0呈現(xiàn)的阻抗；s是由單邊拉普拉斯變換引進(jìn)的復(fù)變量。

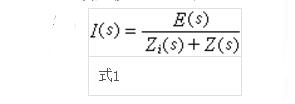
　　和戴維南定理類似，有諾頓定理或亥姆霍茲－諾頓定理。按照這一定理，任何含源線性時(shí)不變二端網(wǎng)絡(luò)均可等效為二端電流源，它的電流J等于在網(wǎng)絡(luò)二端短路線中流過的電流，并聯(lián)內(nèi)阻抗同樣等于看向網(wǎng)絡(luò)的阻抗。這樣，圖1中的電流I（s）一般可按下式2計(jì)算（圖3）

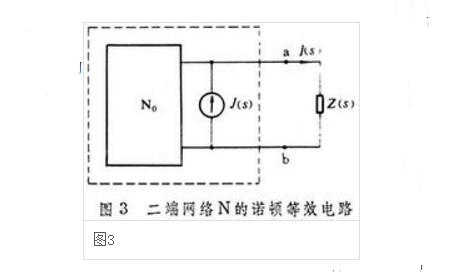
　　式中J（s）是圖1二端網(wǎng)絡(luò)N的短路電流，亦即Z（s）等于零時(shí)的電流I（s）；Zi（s）及s的意義同前。

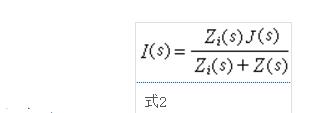
　　圖2、圖3虛線方框中的二端網(wǎng)絡(luò)，常分別稱作二端網(wǎng)絡(luò)N的戴維南等效電路和諾頓等效電路。

　　在正弦交流穩(wěn)態(tài)條件下，戴維南定理和諾頓定理可表述為：當(dāng)二端網(wǎng)絡(luò)N接復(fù)阻抗Z時(shí)，Z中的電流相量I一般可按以下式3計(jì)算式中E、J分別是N的開路電壓相量和短路電流相量；Zi是No呈現(xiàn)的復(fù)阻抗；No是獨(dú)立電源不工作時(shí)的二端網(wǎng)絡(luò)N。

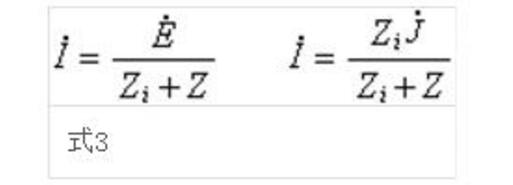
　　這個(gè)定理可推廣到含有線性時(shí)變?cè)�件的二端網(wǎng)絡(luò)。

　　戴維南定理注意事項(xiàng)

　　（1）戴維南定理只對(duì)外電路等效，對(duì)內(nèi)電路不等效。也就是說，不可應(yīng)用該定理求出等效電源電動(dòng)勢(shì)和內(nèi)阻之后，又返回來求原電路（即有源二端網(wǎng)絡(luò)內(nèi)部電路）的電流和功率。

　　（2）應(yīng)用戴維南定理進(jìn)行分析和計(jì)算時(shí)，如果待求支路后的有源二端網(wǎng)絡(luò)仍為復(fù)雜電路，可再次運(yùn)用戴維南定理，直至成為簡(jiǎn)單電路。

　　（3）戴維南定理只適用于線性的有源二端網(wǎng)絡(luò)。如果有源二端網(wǎng)絡(luò)中含有非線性元件時(shí)，則不能應(yīng)用戴維南定理求解。

　　（4）戴維南定理和諾頓定理的適當(dāng)選取將會(huì)大大化簡(jiǎn)電路。

　　應(yīng)用戴維南定理解題

　　戴維南定理的解題步驟：

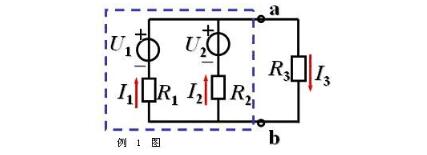
　　1.把電路劃分為待求支路和有源二端網(wǎng)絡(luò)兩部分，如圖1中的虛線。

　　2.斷開待求支路，形成有源二端網(wǎng)絡(luò)（要畫圖），求有源二端網(wǎng)絡(luò)的開路電壓UOC。

　　3.將有源二端網(wǎng)絡(luò)內(nèi)的電源置零，保留其內(nèi)阻（要畫圖），求網(wǎng)絡(luò)的入端等效電阻Rab。

　　4.畫出有源二端網(wǎng)絡(luò)的等效電壓源，其電壓源電壓US=UOC（此時(shí)要注意電源的極性），內(nèi)阻R0=Rab。

　　5.將待求支路接到等效電壓源上，利用歐姆定律求電流。

　　例1：電路如圖，已知U1=40V，U2=20V，R1=R2=4，R3=13，試用戴維寧定理求電流I3。

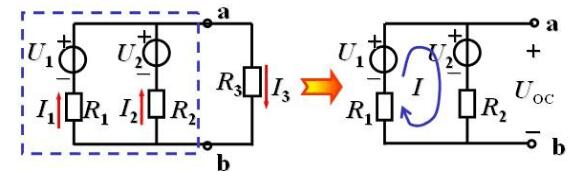
　　解：（1）斷開待求支路求開路電壓UOC

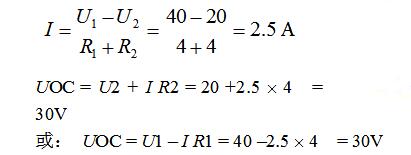
　　UOC也可用疊加原理等其它方法求。

　　（2）求等效電阻R0

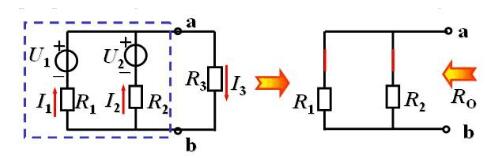
　　將所有獨(dú)立電源置零（理想電壓源用短路代替，理想電流源用開路代替）

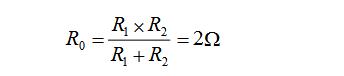
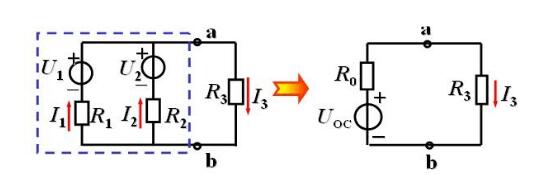
　　（3）畫出等效電路求電流I3

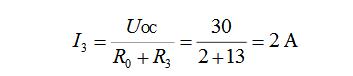
　　例2：試求電流I1

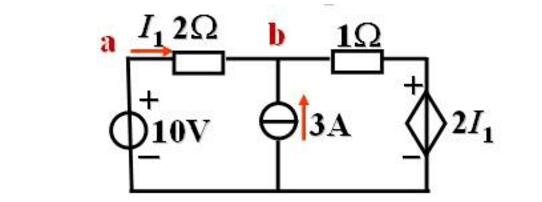
　　解：（1）斷開待求支路求開路電壓UOCUOC=10減去3乘以1=7V

　　（2）求等效電阻R0

　　R0=3

　　（3）畫出等效電路求電流I3

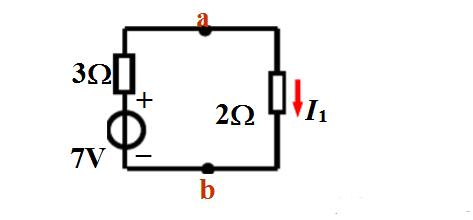
　　解得：I1=1.4A