1.1 基爾霍夫定律是闡明集總參數電路中流入和流出節點的各電流間以及沿回路的各段電壓間的約束關系的定律。1845年由德國物理學家G.R.基爾霍夫提出。集總參數電路指電路本身的最大線性尺寸遠小于電路中電流或電壓的波長的電路,反之則為分布參數電路。基爾霍夫定律包括電流定律和電壓定律。
1.2 基爾霍夫定律的內容:一個輻射體向周圍發射輻射能時,同時也吸收周圍輻射體所發射的能量。在平衡輻射狀態下,該物體的發射總能量等于它的吸收總能量。輻射體在溫度T、波長為λ的總能量與吸收本領的比值等于處在平衡輻射態時吸收總能量,它與物體的性質無關,而是波長和溫度的普適函數。
1.3 基爾霍夫定律的結論:一個發射本領大的輻射體,它的吸收本領也一定大。當吸收系數為1時,表示物體吸收了全部發射到它上面輻射能量,是一個理想的輻射體。只有黑體才能夠在任何溫度下及在任何波長上吸收本領恒為1 。一般輻射體的吸收本領總是小于黑體的,即吸收系數小于1。
2 在基爾霍夫定律中的幾個概念及基爾霍夫定律應用的演算:
1.1 支路:一個二端元件視為一條支路,其電流和電壓分別稱為支路電流和支路電壓。下圖所示電路共有6條支路
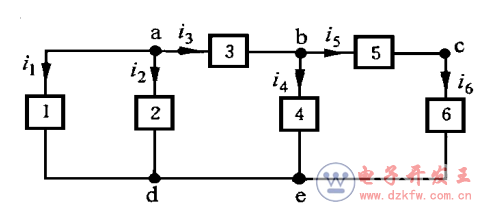
1.2 結點:電路元件的連接點稱為結點。
圖示電路中,a、b、c點是結點,d點和e點間由理想導線相連,應視為一個結點。該
電路共有4個結點。
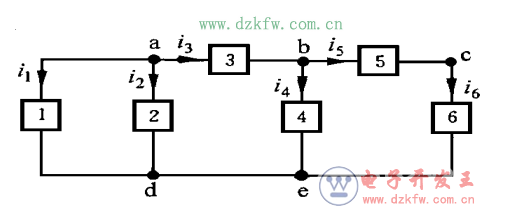
1.3 回路:由支路組成的閉合路徑稱為回路
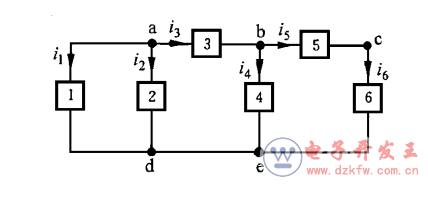
1.4 網孔:將電路畫在平面上內部不含有支路的回路,稱為網孔。
圖示電路中的{1,2}、{2,3,4}和{4,5,6}回路都是網孔
3 基爾霍夫定律的內容:
1.1 基爾霍夫電流定律(KCL)
基爾霍夫電流定律又稱節點電流定律(KCL) 任一集總參數電路中的任一節點,在任一瞬間流出(流入)該節點的所有電流的代數和恒為零,即就參考方向而言,流出節點的電流在式中取正號,流入節點的電流取負號。基爾霍夫電流定律是電流連續性和電荷守恒定律在電路中的體現。它可以推廣應用于電路的任一假想閉合面。
即對任一節點有:∑i =0 。
1.2 基爾霍夫電壓定律(KVL)
基爾霍夫電壓定律(KVL)任一集總參數電路中的任一回路,在任一瞬間沿此回路的各段電壓的代數和恒為零,即電壓的參考方向與回路的繞行方向相同時,該電壓在式中取正號,否則取負號。基爾霍夫電壓定律是電位單值性和能量守恒定律在電路中的體現。它可推廣應用于假想的回路中。
即對任一閉合回路有:∑u =0 。
4 基爾霍夫定律的應用:
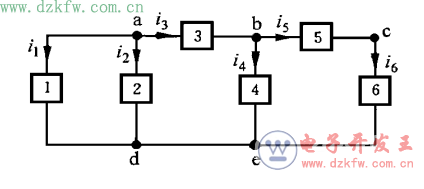
KVL可以從由支路組成的回路,推廣到任一閉合的結點序列,即在任一時刻,沿任一閉合結點序列的各段電壓(不一定是支路電壓)的代數和等于零。對圖l-11電路中閉合結點序列abca和 abda列出的 KVL方程分別為:
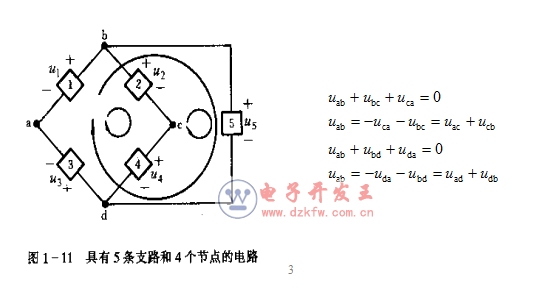
4.1 KVL定律的一個重要應用是:
4.2 根據電路中已知的某些支路電壓,求出另外一些支路電壓,即
集總參數電路中任一支路電壓等于與其處于同一回路(或閉合路徑)的其余支路電壓的代數和,即

由支路組成的回路可以視為閉合結點序列的特殊情況。沿電路任一閉合路徑(回路或閉合結點序列)各段電壓代數和等于零,意味著單位正電荷沿任一閉合路徑移動時能量不能改變,這表明KVL是能量守恒定律的體現。
綜上所述,可以看到:
4.2.1 KCL對電路中任一結點(或封閉面)的各支路電流施加了線性約束。
4.2.2 KVL對電路中任一回路(或閉合結點序列)的各支路電壓施加了線性約束。
4.2.3 KCL和KVL適用于任何集總參數電路、與電路元件的性質無關。
KCL不僅適用于結點,也適用于任何假想的封閉面,即流出任一封閉面的全部支
路電流的代數和等于零。例如對圖示電路中虛線表示的封閉面,寫出的KCL方程
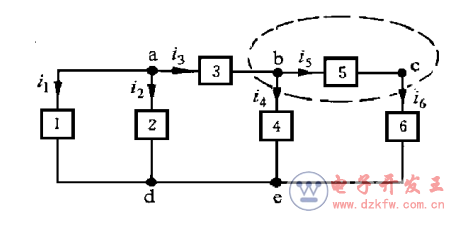

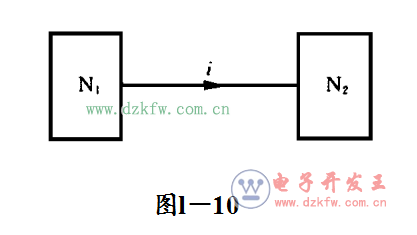
結點的 KCL方程可以視為封閉面只包圍一個結點的特殊情況。根據封閉面 KCL對支路電流的約束關系可以得到:流出(或流入)封閉面的某支路電流,等于流入(或流出)該封閉面的其余支路電流的代數和。由此可以斷言:當兩個單獨的電路只用一條導線相連接時(圖l-10),此導線中的電流必定為零。
在任一時刻,流入任一結點(或封閉面)全部支路電流的代數和等于零,意味著由全部支路電流帶入結點(或封閉面)內的總電荷量為零,這說明KCL是電荷守恒定律的體現
5 在解題方法上的應用
以圖1所示電路為例:來說明基爾霍夫定律在幾種解題方法上的應用,此電路有4個節點,三個網孔,6條支路。
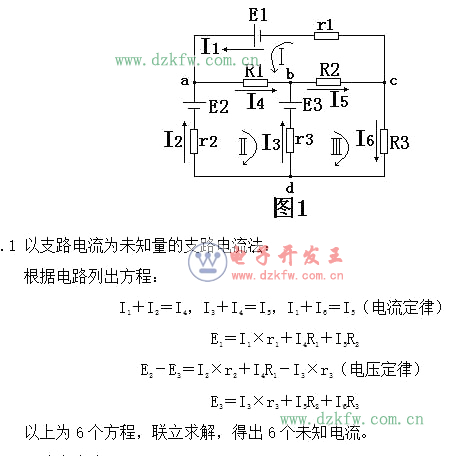
5.2 回路電流法:
根據電路列出方程:
E1=IⅠ(r1+R1+R2)+IⅡR1+IⅢR2
E2–E3=I1R1+IⅡ(r2+ r3+R1)-IⅡ×r3(電壓定律)
E3=IⅠR2- IⅡ×r3+ IⅢ(r3+R2+R3)
以上為3個方程,聯立求解,得出三個電流IⅠ、IⅡ、IⅢ,這三個電流分別為IⅠ= I1,IⅡ= I2,IⅢ= I6,然后應用電流定律可求出另外三個電流。
5.3 節點電壓定律:
根據電路設a點為參考節點,列出方程:
Uao(1/r1+1/r2+1/R1)-Ubo1/R1-Uco1/r1=E2/r2+E1/r1
-Uao1/R1+Ubo(1/R1+1/R2+1/r3)-Uco1/R2=E3/r3(電流定律)
-Uao1/r1-Ubo1/R2+Uco(1/r1+1/R2+1/R3)=-E1/r1
聯立求解方程得節點電壓Uao、Ubo、Uco,然后根據電壓定律求出各知路電流。


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底