一般我們都是采用公式法或者卡諾圖的方法。不過用程序自動化來實現(xiàn)，這兩種方法都不合適。在計算邏輯代數(shù)里面有個叫做Quine-McCluskey（奎因-麥克拉斯基）算法的，用于化簡邏輯公式的，并且它還給出了檢查布爾函數(shù)是否達(dá)到了最小化形式的確定性方法。不過這個算法是NP-完全的，因此運行時間隨輸入變量個數(shù)呈指數(shù)增長。比如邏輯變量個數(shù)有幾十個的時候，這時候找到最簡表達(dá)式已經(jīng)是不太可能，只能通過啟發(fā)式算法（Espresso算法）來尋求次優(yōu)解。

　　根據(jù)輸入端的變化，寫出輸出端的狀態(tài)，真值表就出來了。相反，從輸出端倒推回輸出端，就是邏輯表達(dá)式

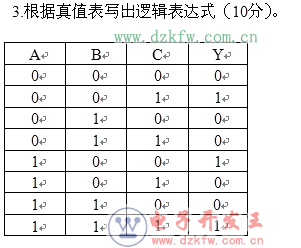
　　第一種方法：以真值表內(nèi)輸出端“1”為準(zhǔn)

　　第一步：從真值表內(nèi)找輸出端為“1”的各行，把每行的輸入變量寫成乘積形式;遇到“0”的輸入變量上加非號。 第二步：把各乘積項相加，即得邏輯函數(shù)的表達(dá)式。

　　第二種方法：以真值表內(nèi)輸出端“0”為準(zhǔn)

　　第一步：從真值表內(nèi)找輸出端為“0”的各行，把每行的輸入變量寫成求和的形式，遇到“1”的輸入變量上加非號。

　　第二步：把各求和項相乘，即得邏輯函數(shù)表達(dá)式。

　　最后化簡，在實際運用過程中，哪個方法簡便就采用哪種。

　　將真值表中函數(shù)值等于1的變量組合選出來；對于每一個組合，凡取值為1的變量寫成原變量，取值為0的變量寫成反變量，各變量相乘后得到一個乘積項；最后，把各個組合對應(yīng)的乘積項相加，就得到了相應(yīng)的邏輯表達(dá)式。 例1120 試根據(jù)表Z1112，寫出相應(yīng)的邏輯表達(dá)式。

　　從表中看到，當(dāng)A＝0、B＝1時，Y＝1；當(dāng)A＝1、B＝0時Y＝1。因此可寫出相應(yīng)的邏輯表達(dá)式為：

　　Y＝B＋A

　　真值表還可用來證明一些定理。

　　例1121 試用真值表證明摩根定理=+

　　證：設(shè)上式左邊 ＝Y(jié)1，右邊＝Y(jié)2，分別列出相應(yīng)的真值表如表Z1113所示：

　　比較Y1和Y2，證得=+。

　　例1122 試用真值表證明A＋AB=A。

　　證：令A(yù)＋AB＝Y(jié)1，A=Y2，列出真值表如Z1114所示。

　　比較Y1和Y2，證得A＋AB=A。