1、半加器
在數學系統中,二進制加法器是它的基本部件之一。
半加器(半加就是只求本位的和,暫不管低位送來的進位數)的邏輯狀態表
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
其中,A和B是相加的兩個數,S是半加和數,C是進位數。
由邏輯狀態表可寫出邏輯式:
![]()
![]()
由邏輯式就可畫出邏輯圖,如下圖(a)和(b)所示,由一個“異或“門和一個”與“門組成。半加器是一種組合邏輯電路,其圖形符號如下圖(c)所示。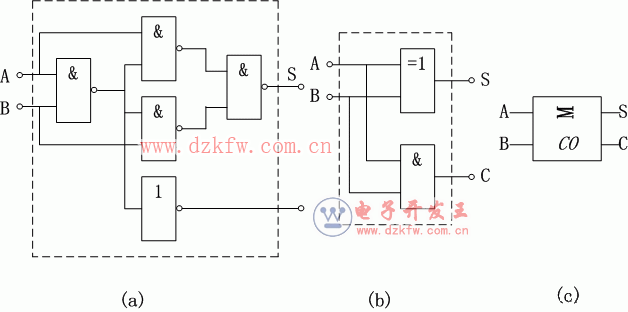
2、全加器
當多位數相加時,半加器可用于最低位求和,并給出進位數。第二位的相加有兩個待加數![]() 和
和![]() ,還有一個來自前面低位送來的進位數
,還有一個來自前面低位送來的進位數![]() .這三個數相加,得出本位和數(全加和數)
.這三個數相加,得出本位和數(全加和數)![]() 和進位數
和進位數![]() .這種就是“全加“,下表為全加器的邏輯狀態表。
.這種就是“全加“,下表為全加器的邏輯狀態表。
| Ai | Bi | Ci-1 | Ci | Si |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
全加器可用兩個半加器和一個“或“門組成。
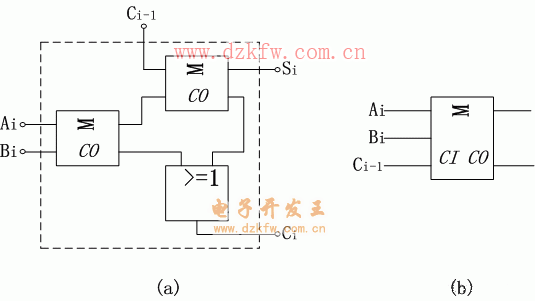
如上圖(a)所示。![]() 和
和![]() 在第一個半加器中相加,得出的結果再和
在第一個半加器中相加,得出的結果再和![]() 在第二個半加器中相加,即得出全加和
在第二個半加器中相加,即得出全加和![]() 。兩個半加器的進位數通過”或“門輸出作為本位的進位數
。兩個半加器的進位數通過”或“門輸出作為本位的進位數![]() 。全加器也是一種組合邏輯電路,其圖形符號如上圖(b)所示。
。全加器也是一種組合邏輯電路,其圖形符號如上圖(b)所示。


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底