一、疊加定理
圖 4.1-1 ( a )所示電路中,有兩個激勵,即獨立電壓源 ![]() 和獨立電流源
和獨立電流源 ![]() ,現欲求 R1 支路上的電流
,現欲求 R1 支路上的電流 ![]() 。
。
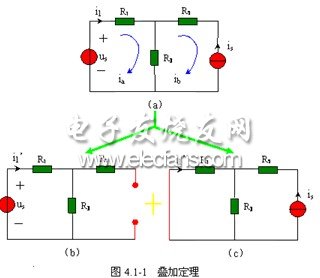
用網孔電流法求解。設網孔電流分別為 ![]() ,其方向都為順時針方向,如圖 4.1-1 ( a )所示。網孔方程為
,其方向都為順時針方向,如圖 4.1-1 ( a )所示。網孔方程為
![]()
解方程得,網孔電流為
![]()
所以, R1 支路電流為
![]()
其中, ![]() 可以看成是當
可以看成是當 ![]() 時的
時的 ![]() 的值,
的值, ![]() 則可看成是當
則可看成是當 ![]() 時的
時的 ![]() 的值。如圖 4.1-1 ( b )、( c )。
的值。如圖 4.1-1 ( b )、( c )。
令
![]()
則
![]()
其中, k1 , k2 是由電路的結構和元件的參數決定的。對于線性電路, R1 、 R2 、 R3 都是常數,不會隨著電路中激勵的數目和大小的改變而改變,所以 k1 , k2 也不會隨激勵的改變而改變,即為常數。 i 是激勵的一次線性函數。
疊加定理
( superposition theorem )
由線性元件組成的線性電路,當 n 個激勵共同作用時,在某條支路上產生的響應,等于各個激勵單獨作用時產生的響應的代數和。
![]()
其中, ![]() 表示 n 個激勵(獨立電壓源或獨立電流源), r 表示某條支路上產生的響應(電壓或電流)。
表示 n 個激勵(獨立電壓源或獨立電流源), r 表示某條支路上產生的響應(電壓或電流)。 ![]() 都是常數,其大小由電路的結構和元件的參數決定。
都是常數,其大小由電路的結構和元件的參數決定。
應用疊加定理時應注意的問題
1 .疊加定理是線性電路的一個重要性質,因此只適用于線性電路,對于非線性電路則不能使用。
2 .當某個激勵單獨作用時,其他激勵均取 0 。將獨立電壓源取 0 ,是把電壓源短路,將獨立電流源取 0 是把電流源開路。
3 .受控源雖然帶有電源的性質,但不直接起激勵作用,因此,在疊加定理中,受控源一般不單獨作用,而是把受控源當電路元件處理。當獨立源單獨作用時,受控源應保留在電路中。
4 .疊加定理只適用于計算電壓或電流,而不適用于計算功率,因為功率與電壓、電流之間的關系不是線性關系。
例 4.1-1 圖 4.1-2 ( a )所示電路,試用疊加定理求 3 Ω電阻上的電壓 U 及功率。
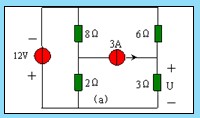
解:電路中有兩個獨立源共同激勵。
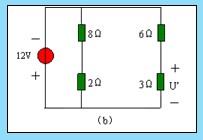
1 、當 12V 電壓源單獨激勵時,電流源應視為 0 ,即把電流源開路,如圖 4.1-2 ( b )所示。
由分壓公式,得
![]()
 |
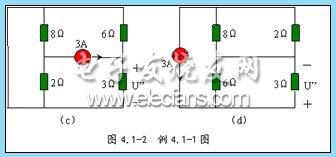
2 、當 3A 電流源單獨激勵時,電壓源應視為 0 ,即把電壓源短路,如圖 4.1-2 ( c )所示。對圖 4.1-2 ( c )電路作變換,得圖 4.1-2 ( d )所示電路。
![]()
3 、當電壓源和電流源共同作用時,由疊加定理得 3 Ω電阻上的電壓
![]()
3 Ω電阻上的功率為
![]()
注 意
計算功率時,不能用疊加定理。
例 4.1-2 用疊加定理計算圖 4.1-3 ( a )所示電路中受控源兩端電壓及功率。
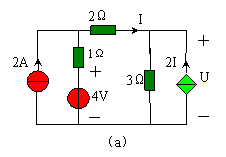 |
解:當 4V 電壓源單獨作用時,電流源視為開路,其電路如圖 4.1-3 ( b )所示,對圖中所示的回路,利用 KVL ,得
![]()
所以,
![]()
則
![]()
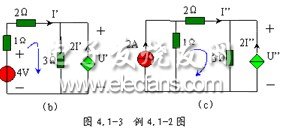
當 2A 電流源單獨作用時,電壓源視為短路,其電路如圖 4.1-3 ( c )所示,對圖中所示的回路,利用 KVL ,得
![]()
所以,
![]()
則
![]()
因此,當電壓源和電流源共同作用時,利用疊加定理得
![]()
受控源兩端電壓為
![]()
受控源的功率為
![]()
二、齊次定理
齊次定理
( homogeneity theorem )
當線性電路中只有一個獨立源作用時,電路的響應與激勵成正比。
推 論:對于線性電路,若所有激勵同時擴大(或縮小) K 倍,則電路中任一支路的響應也擴大(或縮小) K 倍。
例 4.1-3 圖 4.1-4 所示的梯形電路中, Us=6V ,試用齊次定理計算支路電流 I5 。
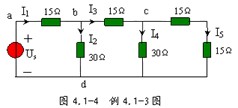
解:這個電路是由電阻的串、并聯組成,可以用等效電路的分析方法進行計算,但是用齊次定理計算會更方便。先設 I5 支路電流為 ![]() ,則
,則
![]()
所以,
![]()
![]()
![]()
故
![]()
![]()
![]()
根據齊次定理,激勵 ![]() 與響應
與響應 ![]() 成正比,即
成正比,即
![]()
因此,
![]()
注 意
應用疊加定理和齊次定理時,當激勵的參考方向反向時,相當于激勵變為原來的- 1 倍。
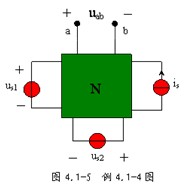
例 4.1-4 圖 4.1-5 所示電路中, N 是不含獨立源的線性網絡,有 3 個獨立源共同激勵, a 、 b 兩端的電壓 ![]() 為 10V 。當電壓源
為 10V 。當電壓源 ![]() 和電流源
和電流源 ![]() 反向而
反向而 ![]() 不變時,
不變時, ![]() 變為 5V ;當電壓源
變為 5V ;當電壓源 ![]() 和電流源
和電流源 ![]() 反向而
反向而 ![]() 不變時,
不變時, ![]() 變為 3V 。試問:只有電流源
變為 3V 。試問:只有電流源 ![]() 反向而電壓源
反向而電壓源 ![]() 和
和 ![]() 不變時,
不變時, ![]() 變為多少?
變為多少?
解:由于是線性電路,所以可用疊加定理。 3 個獨立源共同激勵,電路的響應
![]() ( 1 )
( 1 )
式中, ![]() 為常數,由電路的結構和元件的參數決定。
為常數,由電路的結構和元件的參數決定。
當電壓源 ![]() 和電流源
和電流源 ![]() 反向而
反向而 ![]() 不變時,電路的結構和元件的參數不變,
不變時,電路的結構和元件的參數不變, ![]() 的大小不變,而
的大小不變,而 ![]() 都要乘以系數- 1 ,這時的 a 、 b 兩端的電壓為
都要乘以系數- 1 ,這時的 a 、 b 兩端的電壓為
![]() ( 2 )
( 2 )
又當電壓源 ![]() 和電流源
和電流源 ![]() 反向而
反向而 ![]() 不變時,
不變時, ![]() 乘以系數- 1 , a 、 b 兩端的電壓為
乘以系數- 1 , a 、 b 兩端的電壓為
![]() ( 3 )
( 3 )
(2) + (3) ,得
![]() ( 4 )
( 4 )
所以,當只有電流源 ![]() 反向而電壓源
反向而電壓源 ![]() 和
和 ![]() 不變時, a 、 b 兩端的電壓為
不變時, a 、 b 兩端的電壓為
![]()


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底