>微分形式：在電磁場(chǎng)的實(shí)際應(yīng)用中，經(jīng)常要知道空間逐點(diǎn)的電磁場(chǎng)量和電荷、電流之間的關(guān)系。從數(shù)學(xué)形式上，就是將麥克斯韋方程組的積分形式化為微分形式。利用矢量分析方法，可得：
　　　　　　　
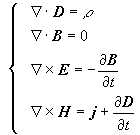
注意：(1)在不同的慣性參照系中，麥克斯韋方程有同樣的形式。
(2) 應(yīng)用麥克斯韋方程組解決實(shí)際問題，還要考慮介質(zhì)對(duì)電磁場(chǎng)的影響。例如在各向同性介質(zhì)中，電磁場(chǎng)量與介質(zhì)特性量有下列關(guān)系：。 在非均勻介質(zhì)中，還要考慮電磁場(chǎng)量在界面上的邊值關(guān)系。在利用t=0時(shí)場(chǎng)量的初值條件，原則上可以求出任一時(shí)刻空間任一點(diǎn)的電磁場(chǎng)，即E(x,y,z,t)和B(x,y,z,t)。
地位：麥克斯韋方程組在電磁學(xué)中的地位，如同牛頓運(yùn)動(dòng)定律在力學(xué)中的地位一樣。以麥克斯韋方程組為核心的電磁理論，是經(jīng)典物理學(xué)最引以自豪的成就之一。它所揭示出的電磁相互作用的完美統(tǒng)一，為物理學(xué)家樹立了這樣一種信念：物質(zhì)的各種相互作用在更高層次上應(yīng)該是統(tǒng)一的。另外，這個(gè)理論被廣泛地應(yīng)用到技術(shù)領(lǐng)域。