一、網孔電流方程
出發點
進一步減少方程數,用未知的網孔電流代替未知的支路電流來建立方程。
圖3.3-1所示電路,共有n=4個節點,b=6條支路(把電壓源和電阻串聯的電路看成一條支路)。顯然,獨立的網孔數為b-n+1=3個。
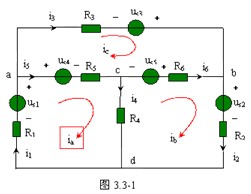
1、網孔電流
設想每個網孔中有一個假想的電流沿著構成該網孔的各條支路循環流動,把這一假想的電流稱為網孔電流(mesh current),如圖3.3-1中的![]() 分別表示網孔a、b、c的網孔電流。電路中各支路電流就可以用網孔電流表示
分別表示網孔a、b、c的網孔電流。電路中各支路電流就可以用網孔電流表示
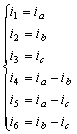
結 論:用3個網孔電流表示了6個支路電流。進一步減少了方程數。
2、網孔電流方程
根據KVL,可得圖3.3-1電路的網孔電流方程
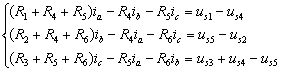
網孔電流方程的一般形式
自電阻×本網孔電流±Σ(互電阻×相鄰網孔電流)= 本網孔中沿網孔電流方向的所有電壓源的電位升之和
自電阻(self resistance)是各網孔中所有支路電阻之和,互電阻(mutual resistance)是兩個相鄰網孔之間的共有電阻。第二項前的正負號由相鄰網孔電流與本網孔電流在互電阻上流過的方向是否一致來決定,若一致取正號;反之取負號。
網孔電流法分析電路的一般步驟
確定電路中的網孔數,并設定各網孔電流的符號及方向。按常規,網孔電流都取順時針或逆時針方向。列寫網孔電流方程,并求解方程,求得各網孔電流。由求得的網孔電流,再求其他的電路變量,如支路電流、電壓等。
例3.3-1 圖3.3-1所示電路中,已知us1=21V,us2=14V,us3=6V,us4=us5=2V,R1=3Ω,R2=2Ω,R3=3Ω,R4=1Ω,R5=6Ω,R6=2Ω,求各支路電流。
解:1. 電路的網孔為3個。設定3個網孔電流的符號及方向如圖3.3-1所示。
2.列寫網孔方程
網孔a: ![]()
網孔b: ![]()
網孔c: ![]()
代入參數,并整理,得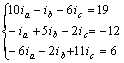
解得網孔電流為: ![]()
3.由網孔電流求各支路電流![]()
![]()
![]()
![]()
2、全歐姆定律
只有一個網孔的電路,稱為單回路電路(single loop circuit)。對于單回路電路,有全歐姆定律。
全歐姆定律:對于單回路電路,回路電流i等于沿回路電流方向的所有電壓源的電壓升的代數和除以回路中所有電阻之和。![]()
二、含有電流源的電路
1、有伴電流源
結 論:如果電路中的電流源是有伴電流源,將有伴電流源等效成有伴電壓源。
方法一 把電流源當電壓源處理
設定電流源兩端的電壓,列寫網孔方程,利用電流源的電流與網孔電流之間的關系再補充一個方程。
2、無伴電流源
電流源處于邊界支路上
結 論:電流源所在網孔的網孔電流即為電流源的電流,因此可以少列一個網孔方程。
例3.3-2 圖3.3-2所示電路中,試用網孔電流法求流過3Ω電阻的電流I1。
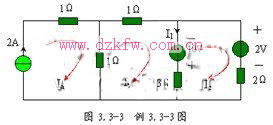
解:電路中含有一個2A電流源,處于網孔a的邊界支路上。取順時針方向為各網孔電流的方向,則![]() (1)
(1)
因此,只需列寫兩個網孔方程,
網孔b: ![]() (2)
(2)
網孔c: ![]() (3)
(3)
經整理后,得![]()
解得網孔電流為: ![]()
所以,流過3Ω電阻的電流為![]()
2)電流源處于相鄰網孔的公共支路上
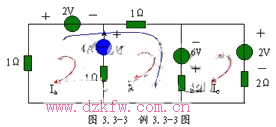
例3.3-3 電路如圖3.3-3所示,試用網孔電流法求各網孔電流。
解:電路中的1A電流源處于網孔a、b的公共支路上。設它的兩端電壓為U,并將它當作電壓源看待,列寫網孔方程,
網孔a: ![]() (1)
(1)
網孔b: ![]() (2)
(2)
網孔c: ![]() (3)
(3)
補充方程: ![]() (4)
(4)
整理后得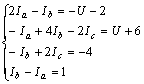
解上述方程組,得網孔電流為![]()
方法二 超網孔(super mesh)方法
把以電流源為公共支路的兩個網孔當作一個超網孔處理,使電流源所在支路不出現在超網孔的支路中。
注 意:列寫超網孔方程時,由于電流源與1Ω電阻串聯的支路沒有出現在超網孔中,所以,這條電流源支路不應計算進去。
利用超網孔的方法計算例3.3-3。
對超網孔: ![]() (1)
(1)
對網孔c: ![]() (2)
(2)
補充方程: ![]() (3)
(3)
整理后得,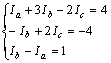
解方程組,得網孔電流為![]()
三、含有受控源電路
思 路:把受控源當獨立源看待。當然,如果受控源的控制量不是網孔電流,應再補充一個能反映控制量與某網孔電流之間關系的方程式。
例3.3-4 電路如圖3.3-4所示,試網孔電流法求受控源發出的功率。
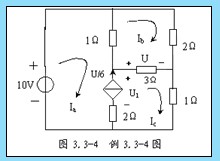
解:電路中有一個受控電流源,而且是無伴電流源,設其兩端電壓為U1,把它當獨立的電壓源看待。
設3個網孔的網孔電流分別為![]() ,其方向均為順時針方向,如圖3.3-5所示,列寫網孔方程,
,其方向均為順時針方向,如圖3.3-5所示,列寫網孔方程,
網孔a: ![]() (1)
(1)
網孔b: ![]() (2)
(2)
網孔c: ![]() (3)
(3)
補充方程: ![]() (4)
(4)![]() (5)
(5)
以上5個方程聯立求解,得![]()
![]()
受控源的電流為 ![]()
所以,受控源發出功率為![]()


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底