流動相似概念

流體運動是自然界普遍存在的現象，與人類的生產生活密切相關，在這些過程中，我們不斷的積累經驗，增加認識。16世紀，達芬奇推導出了一維不可壓粘性流動質量守恒方程，并對波動、漩渦等的形成進行了研究，在這一階段，人們開啟了將流體運動的研究從經驗到科學的轉變，催生了現代流體力學。

流體力學在國民經濟、軍事等諸多領域得到了廣泛的應用，并已經開展了很多深入的研究，在相關分析中，流體相似理論是一個重要的組成。

流動相似理論主要是從實驗中發展而來的，在流體分析中，有一些實驗不允許在真實的環境下進行，或者需要消耗大量的人力、物力和財力，或者部分實驗在真實環境下，反而難以測得所需要的信息，那么，這些時候，就需要通過一定的模型試驗，采用合理的相似理論，抓住問題的本質，來進行分析研究。流動相似理論也成為流體分析中的一個重要概念。

例如，在人類早期的飛行嘗試中，往往都是直接模仿鳥類或者昆蟲的外形和運動方式，但是大都失敗了，這是因為我們過于關注動力學和外形模仿，而沒有考慮流動相似理論中尺度的重要影響。在科幻電影中，一些昆蟲，例如蜜蜂蒼蠅等，變異后變得巨大，在空氣中飛翔，這種場景在現實中是幾乎不可能出現的，因為盡管外形相似，但是比例放大后，因為雷諾數的不同，昆蟲翅膀周圍的流場狀態發生了巨大改變，由層流變成了湍流，導致使其飛行的動力發生了根本變化。

所以，如今的飛行器設計，均要按照流動相似概念進行大量的模型試驗，從本質上說，流動相似，就是要保證控制方程中的各種影響因素相似，例如連續方程、動量方程以及能量方程，通常情況下，我們會在這些方程中總結出無量綱數，作為流體相似分析中的主導參數。例如，雷諾數，馬赫數等等。

常用無量綱數簡介

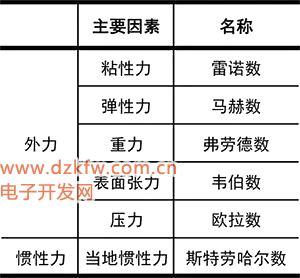
無量綱數大多為某兩種力之比，這是因為流動運動狀態的改變決定于其所受到的力，而哪種作用力占主導因素，流動就主要由該作用力決定。下面列舉的是一部分常用的無量綱數：

 1 雷諾數

式中，ρ為流體密度；V為流速；L為流場中的特征長度，例如圓管的特征尺度即為直徑D，但大部分情況下，特征尺度并不是顯而易見的；μ為動力粘性系數。

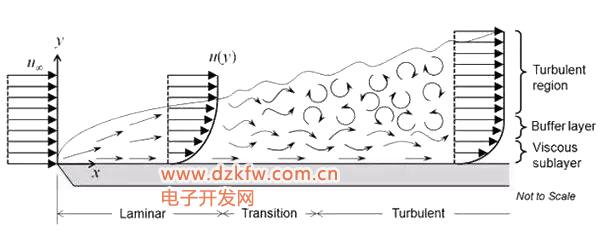
雷諾數可以說是最著名的無量綱數了，決定了大部分的定長、不可壓等流體流動形式。來源于英國科學家雷諾的著名實驗，在該實驗中，水盡量不受擾動地進入圓管，并通過染色劑來觀察水流的狀態，基于此，科學家們發現了一些列臨界雷諾數，其一系列實驗揭示了雷諾數決定著流動狀態是層流還是湍流。

當然，現在來看，這種說法不是十分的準確，嚴格來講，雷諾數的意義是流體的慣性力與粘性力之比，只決定著流體的不穩定度，至于會不會形成湍流，還取決于是否有足夠的擾動觸發，當雷諾數足夠高時，由于微小擾動的不可避免性，流動一定會是湍流，而雷諾數很低時，即使大擾動使流動變成湍流，流體也會自行恢復成層流。因此，通常情況下，可以將雷諾數大致分為以下幾個區間：

• 遠小于1，成為蠕動流，此時慣性力基本可以忽略，物體的運動方式簡單來說就是：有力就動，沒力就停，有點接近于亞里士多德對物體運動方式的描述。例如細菌在液體中移動，毛細血管中的血液流動等等。

  
  

• 雷諾數為1~2100之間，此時，粘性力和慣性力作用不可忽略，流體呈現規則的運動方式，即層流。常見現象例如動脈血管中的血液流動。

  
  

• 雷諾數在2100~105之間，此時，粘性力逐漸減小且變得不穩定，一些小的壓力波動就可能會引起流場長時間的振蕩，因此，流體可能出現層流，也可能是湍流，或是兩者交替。常見現象例如昆蟲與鳥類的飛行，魚類游動等等。

  
  

• 雷諾數大于105，此時慣性力起主導作用，粘性力的影響已經非常小，可以在計算中忽略，流體基本呈現湍流狀態。例如飛行器在空氣中的高速移動，化工行業中反應釜內的攪拌現象等等。

 2 馬赫數

式中，V為流體流速，a為當地聲速。

馬赫數也是十分有名的無量綱數了，尤其在空氣動力學中應用更加廣泛，其意義是物體運動速度與當地的聲速之比，在力的層次上，其表示了流體中慣性力與彈性力之比，馬赫數越大，意味著彈性力的影響就越小，空氣會被拉伸或壓縮，可以類比固體中的彈簧，當彈性模量很小時，彈簧就可以被強烈的進行拉伸與壓縮。

生活中多數常見的流動速度都遠低于聲速，所以馬赫數的影響很小，但是在計算飛行器以及賽車等高速流動時，則通常需要保證馬赫數的一致。例如高速風洞實驗中的流體，一個典型的問題就是激波現象的出現，此時彈性力與粘性力共同影響流體的流動狀態，所以在相關實驗時，要保證雷諾數和馬赫數均一致。此外，當馬赫數很高的時候，雷諾數的影響也幾乎可以忽略，也就是說，當壓縮性的影響變得明顯，粘性的影響就減輕了很多。

 3 斯特勞哈爾數

式中，f為周期性流動的頻率，L為特征長度，V為流體流速。

當流體繞物體流動時，經常會在其后面形成周期性的渦脫落，稱為卡門渦街，對于比較標準的圓柱擾流來說，這種渦脫落現象存在很強的周期性，產生的聲音就像在“唱歌”，斯特勞哈爾正是在研究這種現象時定義了這個無量綱數。當流體做周期性非定常運動時，可以用該量來描述振蕩的程度，它表示了當地慣性力與對流慣性力的比值，數值越大，則振蕩強度越大。

 4 弗勞德數

式中，V為流體流速，g為重力加速度，L為特征長度。

英國科學家弗勞德在研究船舶航行時所遇到的水面波阻力時定義了弗勞德數，它表示了流動中慣性力與重力的比值，一般情況下，在處理重力場內液體的自由表面相關的運動時，會考慮該數值。不過，在大多數流體問題中，重力都是可以忽略的。

 5 歐拉數

式中，p為流體壓力，ρ為流體密度，V為流體流速。

歐拉數表示了流體的壓力與慣性力之比，同時，也是壓力系數的另一種表現形式，在不可壓縮流動中，歐拉數表示了某兩點壓差與來流動壓頭的比例關系。根據伯努利方程，歐拉數也表示了流體的加減速程度。

 6 韋伯數

式中，ρ為流體密度，V為流體流速，L為特征長度，σ為液體的表面張力系數。

韋伯數表示了慣性力與表面張力的比值。在液體的表面會存在表面張力，當流體的運動速度較小，或者液滴的尺度很小時，表面張力就有可能與當地的慣性力相當或者更大，此時就需要考慮表面張力的作用。

韋伯數越小表示表面張力越重要，當韋伯數遠大于1時，表面張力的作用就可以忽略。此外，在某些情況，例如液滴在高速氣流中的破碎問題，發動機在燃燒室中組織高效燃燒問題等，則和韋伯數密切相關。

運用相似理論的流動分析

從理論上來講，想要通過相似理論來分析流動現象，除了在幾何尺寸上保持相似之外，還需要滿足一系列無量綱數的相等。這在實際操作中，幾乎是不可能的，所以，我們往往會根據實際情況，抓住主要變量，進而忽略其他次要影響。

舉例來說，對于常見的低速不可壓縮流動，往往不需要考慮馬赫數的影響，只需要關注雷諾數是否相等，在此基礎上設計模型試驗，例如：常見的風洞實驗，當某巨型設備的周邊真實流場過大，不能放入風洞中計算分析，則需要進行比例縮放處理，并根據相似理論保證流體的雷諾數相當，即可以得到與真實情況相似的計算結果。

對于一些高速空氣動力學實驗，壓縮性的影響是第一位的，流場中往往會形成激波，想通過相似手段在亞音速條件下形成這種情況是不可能的，這時候，可以采取一些聲速低的流體來近似替代。例如，在早期超音速壓氣機實驗時，由于解決不了高速旋轉下葉片的強度和振動問題，遂采取氟利昂作為工作介質，由于聲音在氟利昂中的傳播速度遠小于空氣中，所以可以實現用低轉速模擬高轉速的目的。

如上所示，流體的相似問題理論雖然簡單，但是實現起來卻經常會有各種各樣的問題，很多時候選取的無量綱數無法保證完全相等，這就需要我們在實際操作中，利用更多科學的近似方法來指導流體實驗的設計，如人工轉捩創造湍流，同時可以采取計算機輔助設計的手段，進行流場的仿真計算，對實驗進行指導與參考。